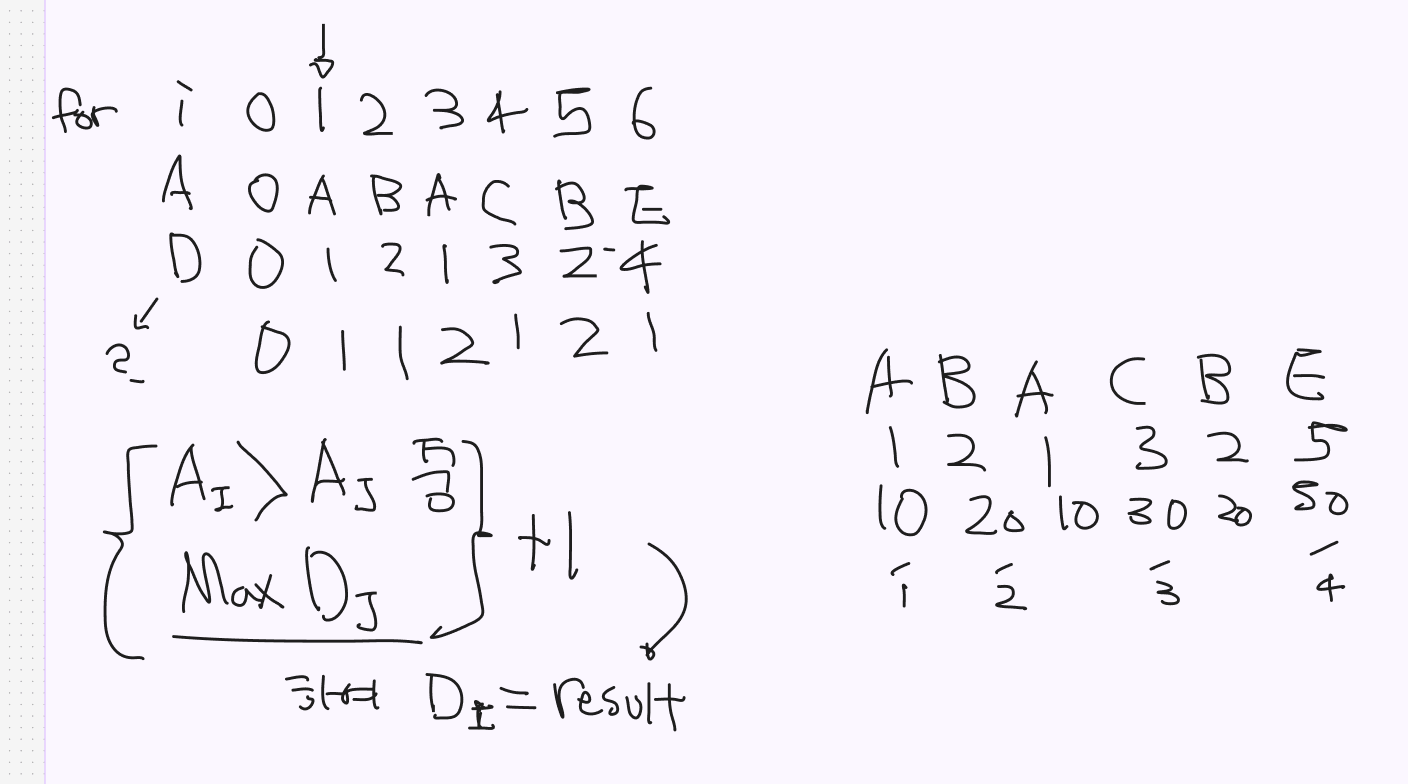포스트

LIS

게시 업데이트
Preview Image
By mascari4615
7 분읽는 시간
LIS

LIS

Longest Increasing Subsequence최장 증가 부분 수열

DP로 풀 수 있는 문제.
수열에서 가장 긴 증가 부분 수열을 찾는 문제.

용어 정리

부분 수열
= 수열의 원소 중 일부를 선택해서(혹은 제거해서) 만든 수열
i.e. 1 2 3 4에서 1 3 4, 2 4 등

증가 부분 수열
= 오름차순으로 정렬된 부분 수열
i.e. 1 2 3 4, 3 5 7 9 등

최장 증가 부분 수열
= 가장 긴 증가 부분 수열

알고리즘

LIS

O(N^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

const int MX = 1005;
int a[MX];
int d[MX];

int main()
{
    int n;
    cin >> n;

    for (int i = 1; i <= n; i++)
        cin >> a[i];

    int mxLen = 0;
    for (int i = 1; i <= n; i++)
    {
        int curA = a[i];
        int curDMax = 0;

        for (int j = 0; j < i; j++)
        {
            int tarA = a[j];
            int tarD = d[j];

            if (tarA < curA)
                if (tarD >= curDMax)
                    curDMax = tarD;
        }

        d[i] = curDMax + 1;
        mxLen = max(mxLen, d[i]);
    }

    cout << mxLen;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

int n;
cin >> n;

vector<int> a(n);
vector<int> d(n);

for (int i = 0; i < n; i++)
    cin >> a[i];

for (int i = 0; i < n; i++)
{
    d[i] = 1;
    
    for (int j = 0; j < i; j++)
        if (a[j] < a[i] && d[i] < d[j] + 1)
            d[i] = d[j] + 1;
}

cout << *max_element(d.begin(), d.end());

O(N log N)

O(N^2) 방법을 최적화하여 O(N log N)으로 만들 수 있다.

O(N^2) 방법은 해당 시점에서 가장 긴 증가 부분 수열의 길이를 계산하고 갱신하는 방식이라면,

O(N log N) 방법은 해당 시점에서 만들 수 있는 가장 긴 증가 부분 수열을 자체를 만들어 갱신하는 방식이다.
O(N log N) 방법은 해당 시점에서 만들 수 있는 가장 긴 증가 부분 수열을 만들어 갱신하는 방식이다.
최종 결과물이 lis가 되지는 않는다, 최종 결과물의 길이가 lis의 길이가 된다.

이진 탐색 (lower_bound)를 이용하여,
해당 시점에 만들어진 증가 부분 수열의 마지막 값보다 큰 값이 나오면 그 값을 추가하고,
작은 값이 나오면 lower_bound로 작은 값이 대체할 수 있는 위치를 찾아 대체한다.

(뭔가 설명이 직관적이진 않다. 까먹었다면 코드 보면서 이해할 것.)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

int n;
cin >> n;

vector<int> a(n);
for (int i = 0; i < n; i++)
    cin >> a[i];

// 해당 시점에서 만들 수 있는 가장 긴 증가 부분 수열, 그 중에서 요소들의 값이 가장 작은 수열을 만들어 나간다.
vector<int> lis;
for (int i = 0; i < n; i++)
{
    // 이진 탐색으로 a[i]보다 크거나 같은 값이 있는지 확인 (그 중 가장 왼쪽에 있는 값)
    // 여기서는 일단 a[i]보다 큰 값을 찾고, 그걸 a[i] 대체하고 싶다는 생각
    auto it = lower_bound(lis.begin(), lis.end(), a[i]);

    // 없으면 뒤에 추가
    if (it == lis.end())
    {
        lis.push_back(a[i]);
    }
    // 있으면 그 값을 a[i]로 교체
    else
    {
        *it = a[i];

        // 교체하는 이유는 전체적으로 요소들의 값이 작아야 나중에 더 긴 증가 부분 수열을 만들 수 있는 가능성이 높아지기 때문
        
        // 예를 들어 5 1 2라는 수열에서, 각 요소를 순회하며 LIS를 구한다고 가정
        // 5까지 순회를 하고, (현재 LIS는 {5})
        // 1를 순회하는 차례에서,
        
        // 5를 1로 바꿔도 어차피 길이는 똑같다고 5를 그대로 두면 최종적으로 LIS를 {5}로 만들 수 밖에 없다.
        // 왜냐하면 2는 5보다 작아서 못 들어가니까.
        
        // 만약 5를 1로 바꿨다면, {1}로 시작하는 LIS를 만들 수 있고
        // 그 다음 2를 순회하는 차례에서, {1}에 2를 추가하면 {1, 2}로 LIS를 만들 수 있다.
    }
}

cout << lis.size();

주석 없는 코드.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

int n;
cin >> n;

vector<int> a(n);
for (int i = 0; i < n; i++)
    cin >> a[i];

vector<int> lis;
for (int i = 0; i < n; i++)
{
    auto it = lower_bound(lis.begin(), lis.end(), a[i]);
    if (it == lis.end())
    {
        lis.push_back(a[i]);
    }
    else
    {
        *it = a[i];
    }
}

cout << lis.size();

기록

문제

컴퓨터, 알고리즘
알고리듬 Dynamic-Programming
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.